Exploring Boolean Operations in SDFs: Union, Difference, and Intersection

In our previous explorations of Signed Distance Functions (SDFs), we unveiled their power in representing and manipulating geometric shapes. We also delved into the intricacies of SDFs for lines and rectangles. Now, let’s unlock the potential of Boolean operations on SDFs, enabling the creation of even more complex shapes.

Merging Shapes with Union: A Powerful Tool

The Union operation in SDFs allows us to combine two or more shapes, essentially merging them into a single new shape. Mathematically, the union of two SDFs, $SDF_1$ and $SDF_2$, representing shapes A and B respectively, can be expressed as:

$$ SDF_{Union}(P) = min(SDF_1(P), SDF_2(P)) $$

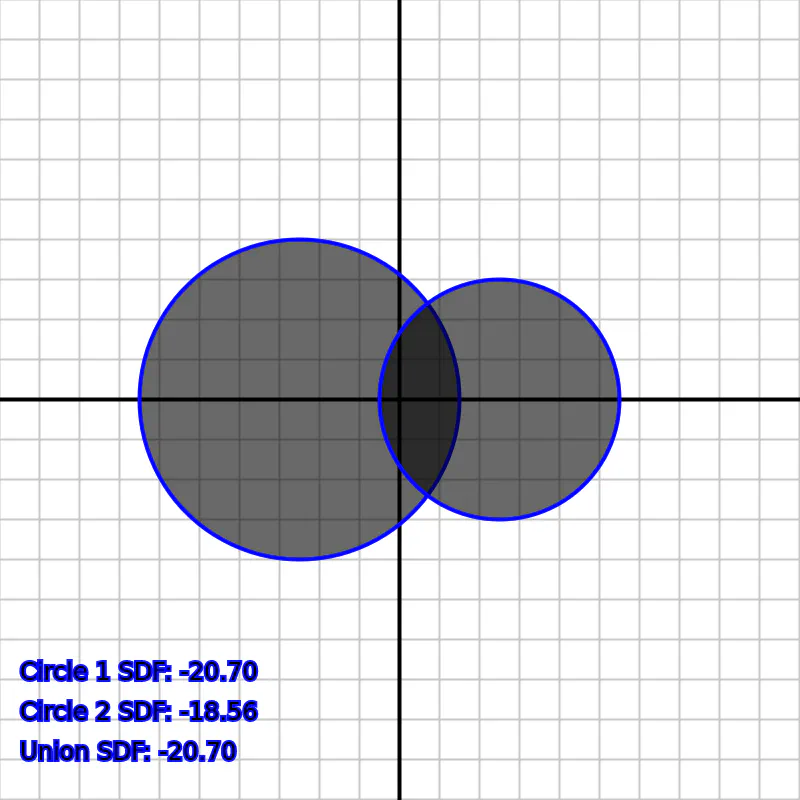
This operation essentially takes the minimum distance value from either SDF at each point (P). Points outside of both shape A or B will have a positive SDF value, indicating they lie outside the combined shape. Points within both shapes A and B will have a negative value, signifying their position inside the resulting union shape.

Union of Two Circles

The visualization of the union of two circles SDF is also available at union_sdf.py using py5 module.

Carving Shapes with Difference: Subtracting One from Another

The Difference operation in Signed Distance Functions (SDFs) enables us to sculpt one shape by subtracting another. Mathematically, the difference of $SDF1$​ and $SDF2$​, representing shapes A and B respectively, can be defined as:

$$ SDF_{Difference​}(P)=max(SDF_1​(P),−SDF_2​(P)) $$

Here, the negative of $SDF_2$​ is taken prior to the maximum operation. This action effectively reverses the sign of distances originating from shape B. Points lying outside both shapes, as well as points residing inside shape A but also within shape B, will yield a positive SDF value. This indicates that they belong to the exterior of the resultant shape after the difference operation. Points situated within shape A but outside shape B will generate a negative value, denoting their inclusion within the final difference shape.

Difference of Two Circles (Circle 1 - Circle 2)

The visualization of the difference of two circles SDF is also available at diff_sdf.py using py5 module.

Finding the Common Ground: Intersection of Shapes

The Intersection operation in SDFs allows us to identify the region where two shapes overlap. Mathematically, the intersection of $SDF_1$ and $SDF_2$ can be expressed as:

$$ SDF_{Intersection}(P) = max(SDF_1(P), SDF_2(P)) $$

In this case, the maximum distance value is taken. Points outside both shapes A and B will have positive SDF values. Points inside either shape A or B (but not their overlap) will also have positive values. Points that lie within the overlapping region of both shapes A and B will have a negative SDF value, signifying their location within the intersection.

Intersection of Two Circles

The visualization of the intersection of two circles SDF is also available at intersect_sdf.py using py5 module.

A Composition of Lines: The SDF of a Rectangle

While we’ve explored circles and other shapes, it’s important to remember that even seemingly basic shapes can be constructed using SDFs and Boolean operations. Take a rectangle, for instance. We can define a rectangle as the intersection of four lines, each representing the distance to an edge:

• The distance to the top edge of the rectangle.
• The distance to the bottom edge.
• The distance to the left edge.
• The distance to the right edge.

Rectangle SDF

The visualization of the rectangle defined by intersection of 4 lines is also available at rect_by_intersect_sdf.py using py5 module.

The order of these intersections does not matter. Taking the maximum distance (intersection) from all four lines simultaneously would define a rectangle. Alternatively, we can perform the intersection progressively.

This concept extends beyond rectangles. Any polygon can be defined similarly using the intersection of line SDFs representing distances to its edges.

Defining Complex Domains with SDF Boolean Operations

By mastering Boolean operations on SDFs, we unlock the ability to create mathematically defined representations of even intricate 2D domains. From simple geometric shapes to elaborate, user-defined patterns, these techniques empower us to model a vast array of scenarios. This opens doors for various applications, from scientific simulations to artistic expression, all leveraging the power of mathematics and code to define complex shapes and spaces.