Demystifying Signed Distance Functions

In the realm of mathematics and computer graphics, signed distance functions (SDFs) play a pivotal role in representing and manipulating geometric shapes. Unlike traditional polygonal meshes, which store vertices and connectivity information, SDFs define shapes implicitly, offering a powerful and flexible approach to 3D modeling and simulation.

What is a Signed Distance Function?

At its core, an SDF is a mathematical function that assigns a real number to each point in space, representing the distance from that point to the nearest boundary of a specified shape. This distance value carries a sign, indicating whether the point lies inside, outside, or on the boundary of the shape.

Properties of Signed Distance Functions

• Non-parametric Representation: SDFs describe shapes without explicit geometric data, making them ideal for representing complex shapes and adapting to deformations.

• Global Shape Representation: SDFs provide a global representation of a shape, allowing for efficient proximity queries and intersection detection crucial for computational geometry.

• Differentiable: SDFs are differentiable, enabling smooth transitions between different shape representations and their derivatives, a key aspect in mesh generation.

Applications of Signed Distance Functions

• Mesh Generation for Physics Simulations: SDFs are widely used in physics simulations to represent objects and their interactions, enabling the creation of high-quality meshes representing objects with complex shapes, realistic collision detection and physics calculations.

• Level of Detail (LOD): SDFs facilitate efficient LOD management by allowing for the creation of high-quality representations at various levels of detail.

• Procedural Modeling: SDFs are the foundation of procedural modeling techniques, enabling the creation of organic and complex shapes from simple mathematical rules.

• Graphics Rendering: SDFs play a crucial role in ray tracing algorithms, enabling ray casting and intersection detection for realistic graphics rendering.

Understanding the Mathematical Significance

In mathematical terms, the sign of the distance values generated by the SDF holds crucial information about the relative position of a point to the shape:

• Negative Values: Points with negative SDF values lie inside the shape’s boundary. The magnitude of the negative value represents how far inside the point is relative to the nearest surface.

• Positive Values: Points with positive SDF values are located outside the shape. Similar to negative values, the magnitude indicates the distance from the point to the nearest surface outside the shape.

• Zero Value: A point with an SDF value of zero resides exactly on the shape’s boundary.

Mathematically, the SDF function can be represented as follows for a given point $P$ in space:

$$ SDF(P) = \text{Distance from } P \text{ to the nearest surface} $$

The sign of $SDF(P)$ provides a concise indication of whether the point $P$ is inside, outside, or on the boundary of the represented shape.

This mathematical understanding is foundational for computational geometry algorithms and plays a pivotal role in mesh generation processes, guiding the placement of vertices and defining the geometry of the resulting mesh.

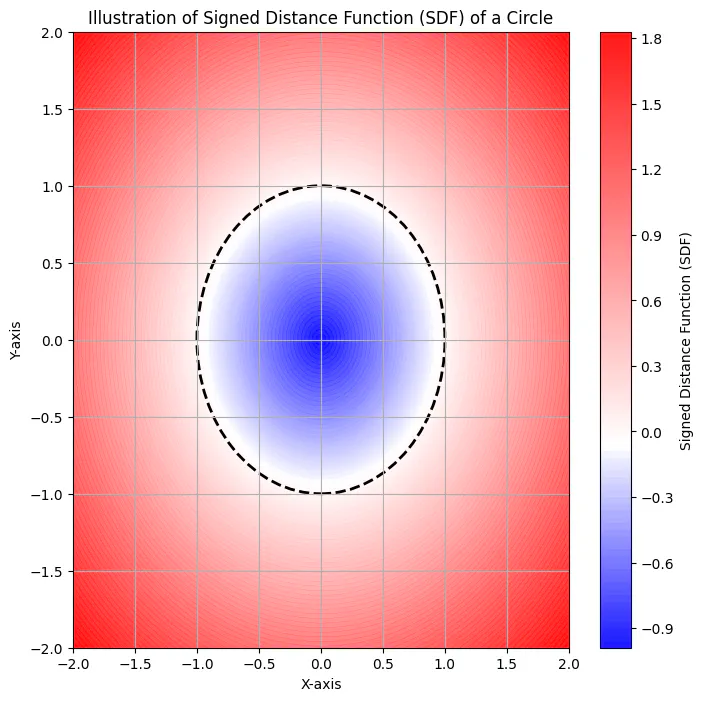
Mathematical Example: SDF for a Circle

Consider a two-dimensional space ($x, y$) and a circle centered at the origin with a radius of $r$. The SDF for this circle ($SDF_{\text{circle}}$) at a given point $(x, y)$ can be expressed as follows:

$$ SDF_{\text{circle}}(x, y) = \sqrt{x^2 + y^2} - r $$

In this equation:

• $SDF_{\text{circle}}(x, y)$ is the signed distance function for the circle.
• $\sqrt{x^2 + y^2}$ calculates the Euclidean distance from the point $(x, y)$ to the origin.
• $r$ is the radius of the circle.

Now, let’s break down the sign of $SDF_{\text{circle}}(x, y)$ based on the relative position of the point to the circle:

• If $SDF_{\text{circle}}(x, y) < 0$, the point $(x, y)$ is inside the circle.
• If $SDF_{\text{circle}}(x, y) > 0$, the point $(x, y)$ is outside the circle.
• If $SDF_{\text{circle}}(x, y) = 0$, the point $(x, y)$ is exactly on the boundary of the circle.

This mathematical example illustrates how the SDF values can be computed for a simple geometric shape like a circle, forming the basis for more complex computations in computational geometry and mesh generation.

Example Python Code: Creating a Circle SDF

The following Python code defines an SDF function for a circle:

1import numpy as np
2
3def circle_sdf(x, y, center = [0,0], radius = 80):
4    return np.sqrt((x - center[0])**2 + (y - center[1])**2) - radius

This function takes two-dimensional coordinates as input and returns the distance from the point to the circle’s boundary.

Signed Distance Function Visualization

The visualization of circle SDF is also available at circle_sdf.py using py5 module.